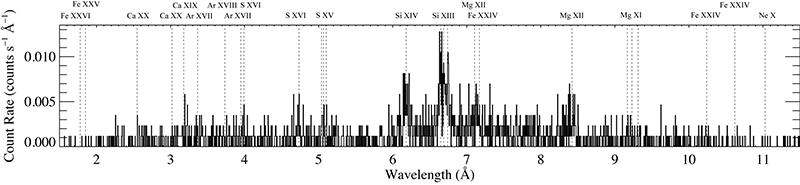
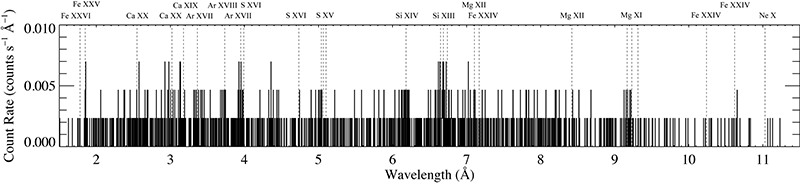
CEN1A: Chandra grating spectrum
The data shown here are from James MacArthur's final extraction (5 May 2010), using Pat Broos's software, and carefully separating the dispersed spectra of the two components (A + B), using narrower-than-usual extraction apertures. This reduction includes GTO data as well as the GO data. The total exposure time is 172.2 ks. James did this work under Marc's supervision.
The ACIS image, light curves, and spectra - from a separate, earlier observation - are shown in this image from the Chandra observing proposal.
Component A - whose data are shown here - is the somewhat dimmer source to the SW. These the MEG and HEG (first order, coadded -1 and +1) spectra. There are 1945 MEG counts and 1059 HEG counts in the first order spectra.
The HETGS spectra
MEG
HEG
Spectral Fits
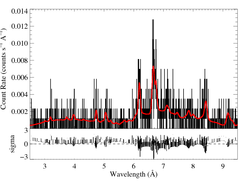
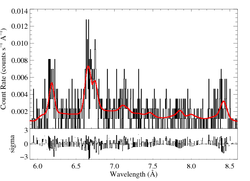
global fit (2-T apec)
The above plot shows the entire range of data that we fit (2.5 to 9.5 A). We also fit the HEG data, simultaneously, but it's not worth the space to show the fit. Because most of the flux is in the central part of this spectral region, we just show 5.9 to 8.6 Angstroms, below.
global fit (2-T bapec)
|
kT1 = 0.47 keV +/- (0.44:0.51) norm1 = 3.38e-3 +/- (2.37e-3:4.57e-3) kT2 = 2.38 keV +/- (2.22:2.53) norm2 = 1.53e-3 +/- (1.36e-3:1.69e-3) v = 1544 km/s +/- (1392:1675) abund = 0.90 solar +/- (0.75:1.11) NH = 2.97e22 cm-2 +/- (2.77e22:3.16e22) rejection probability = ???% (C=5930.86; N=8396) |
This fit is good. Its ISM column density is reasonable given AV = 10 mag. The line widths are high - consistent with embedded wind shocks, but on the high side for colliding wind shock emission. The temperature distribution is not all that high. The hot component emission measure is 40% of the cooler component's. I have not included windtabs in the fitting. The ISM column is so high (almost 10 times HD 93129's) that I don't think wind absorption will dominate. But here, as with HD 93129, the spectrum is hard largely due to absorption, rather than intrinsically very hard emission and very high temperatures (although the intrinsic plasma emission temperature is higher than that seen in HD 93129).
[I also fit a one temperature model to these data. The fit was not as good. ΔC = 180. You can see that while the continuum is fit pretty well, the main line ratio (Si XIII vs. Si XIV at 6.7 and 6.2 Angstroms) is not as well fit as in the 2-T fit above.]
The unabsorbed flux in the best-fit 2-T model corresponds to an X-ray luminosity of 2.0e33 ergs/s, about a factor of 3 higher than the Lx for HD 93129. But it is somewhat lower than the 3e33 that Marc found from fitting the earlier ACIS spectra. Note also that Marc's fit gave somewhat higher temperatures and used a lower ISM column density.
In summary, the plasma temperature and X-ray luminosity are both quite high; more likely to be of CWS origin than EWS origin, but EWS cannot be completely ruled out based on these fits to the broadband data alone.
The very large line widths found in the bapec modeling are, however, somewhat more like what's expected from EWS X-rays, and suggests that we might try fitting windprofile models.
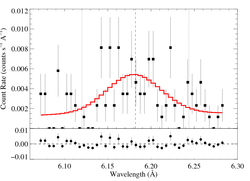
6.182 Angstroms: Si XIV Ly-alpha
But first, we fit this line with a wgauss + powerlaw model. The MEG and HEG data were fit simultaneously. The dashed vertical line is the rest wavelength of the line, and the two dotted vertical lines represent Doppler shifts of +/- 3000 km/s (arbitrarily; we don't know the wind properties of this star or stars).
Note that the fit shown below is new as of January 20, 2012. It uses a somewhat wider range of wavelengths over which to fit the line. My old fit on [6.10:6.26] Angstroms gives results consistent with this fit. And you can compare the results shown here for CEN1A to Sierra's wgauss+pow fit to the same line in the spectrum of CEN1B. Both the line and continuum are several times stronger, but component B shows similar broadening and lack of evidence for a blue-shifted centroid.
wgauss + pow
MEG
HEG 
|
fit on [6.07:6.29] continuum powerlaw n = 2, norm = 1.75e-4 continuum fit on 5.95:6.10 & 6.30:6.45 A wavelength = 6.182 A sigma = 30.37 mA +/- (25.18:37.27) corresp. to 1393 km/s +/- (1182:1672) delta = -1.84 mA +/- (-7.57:3.71) corresp. to -88 km/s +/- (-345:171) norm = 3.05e-6 +/- (2.52e-6:3.46e-6) rejection probability = ???% (C=242.21; N=260) |
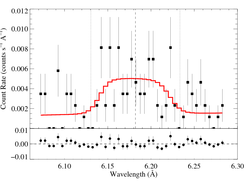
This fit is reasonable, especially given the low quality of the data. But to what extent can a standard EWS-appropriate wind profile model be ruled out? The best-fit Gaussian is a little blue shifted, but not significantly. It is broad -- the vertical lines are at 3000 km/s. We'll fit windprofile + powerlaw and see what constraints we can put on taustar. Keeping in mind that we don't know the wind properties of the star, but that the star is very hot, and keeping in mind, also, that the line is quite broad, we'll try two values of the terminal velocity, 3000 km/s and 2500 km/s.
windprof + pow
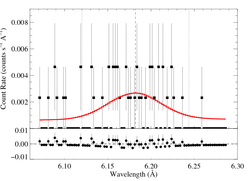
For the higher terminal velocity of 3000 km/s:
MEG
|
fit on [6.07:6.29] continuum powerlaw n = 2, norm = 1.75e-4 wavelength = 6.182 A taustar = 0.04 +/- (0.00:0.50) Ro = 2.04 R* +/- (1.73:2.54) norm = 2.80e-6 +/- (2.41e-6:3.23e-6) rejection probability = ???% (C=240.73; N=260) |
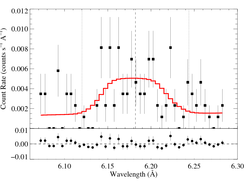
And for the lower terminal velocity of 2500 km/s:
MEG
|
fit on [6.07:6.29] continuum powerlaw n = 2, norm = 1.75e-4 wavelength = 6.182 A taustar = 0.14 +/- (0.00:1.32) Ro = 3.16 R* +/- (2.25:5.93) norm = 2.80e-6 +/- (2.38e-6:3.19e-6) rejection probability = ???% (C=240.32; N=260) |
There's no evidence compelling us to believe that there are wind absorption effects evident in the observed line profile. Although, significant taustar values cannot be ruled out, especially for the lower assumed terminal velocity. This line has a taustar value of 0.5 in zeta Pup's spectrum, by the way.
The Gaussian and each wind profile model provide fits that are statistically equivalent (at the 90% confidence limit).
My old fit on [6.10:6.26] Angstroms gives results consistent with these fits.
Points and items still to do
The circumstantial evidence from these grating data alone point toward CWS as the primary X-ray production mechanism -- Plasma emission levels and temperatures too high to be EWS (though this is not definitive), no compelling evidence for shifted and skewed profiles indicative of EWS (though the limits on this are not highly constraining). MCWS also seems unlikely, due to the very broad lines.
The steady rise in the light curve seen in the old ACIS data (see image from proposal linked at the top of this page) is also indicative of CWS emission.
There are one or two weaker emission lines we can also fit.
And we have still to refit the f/i ratio in the Si XIII complex. We don't expect the constraints to be especially stringent, based on our initial fits. But those earlier fits did show the ratio possibly lowered from the normal ("high density limit") value. The modest X-ray emission temperatures we find (compared to CEN1B) might be understood if the binary separation is not too great (which might also then explain any lowered f/i ratios).
A detailed log of all the fitting reported on here is available.
New (as of 10 Apr 11): I've now done the three-Gaussian fitting to the Si XIII He-like complex, with results shown below.
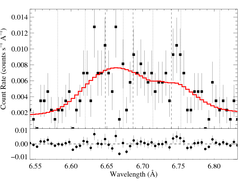
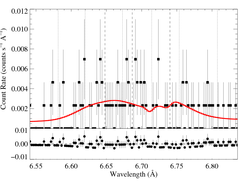
6.7 Angstroms: Si XIII helium-like res., int., for.
These data were fit with a hegauss + powerlaw model. The MEG and HEG data were fit simultaneously.
MEG
HEG 
|
fit on [6.54:6.84] continuum powerlaw n = 2, norm = 1.79e-4 wavelength = 6.6479, 6.6866, 6.7403 A R = f/i = 1.21 +/- (0.49:2.78) G = (f + i)/r = 1.26 +/- (0.64:2.57) sigma = 1474 km/s +/- (1197:1892) delta = -93 km/s +/- (-566:490) norm = 7.15e-6 +/- (6.56e-6:7.83e-6) rejection probability = ???% (C=336.37; N=356) |
This fit is statistically good, but doesn't provide very strong constraints. The best-fit R is low, but the 68% confidence limit encompasses Ro (the low-density limit); and higher values of R are favored when G is at the low end of the confidence range (which is more in line with theoretical expectations). Incidentally, the vertical dotted lines are at +/-3000 km/s, somewhat arbitrarily. They're irrelevant to the Gaussian fits, though; just there to provide context.
last modified: 24 January 2012