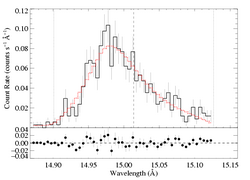
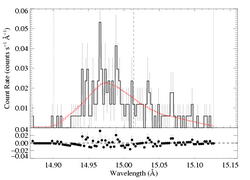
Fe XVII 15.014 Angstroms

Non-porous models

Note: Both MEG and HEG are being fit simultaneously

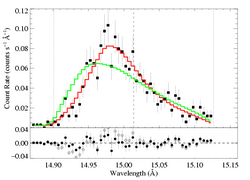
Continuum fit on 14.85:14.90. For n=2, best-fit norm=1.71e-3. The 68% confidence limits on the normalization are approx. +/-0.5e-3. And the best fit is formally a good fit.

[14.87:15.13]
v_inf=2250
β=1
powerlaw continuum, n=2; norm=1.71e-3
q=0
h_inf=0
taustar=1.94 +/- (1.61:2.26)
u_o=0.646 +/- (0.596:0.700)
norm=5.24e-4 +/- (5.08e-4:5.49e-4)
rejection probability = 26% (C=280.83; N=308)

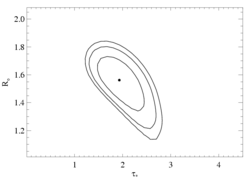
Here are the 68%, 90%, and 95% joint confidence limits on taustar and R_o based on fitting the MEG and HEG data together. The filled circle represents the best-fit model, shown as the red histograms on the above two plots.

New (2Jan09): note that we've now begun plotting these 2-D confidence contour plots in terms of R_o rather than u_o.

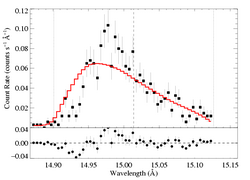
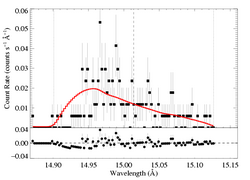
The literature mass-loss rate implies a fiducial optical depth at the wavelength of this line of about taustar=5.30 (using kappa = 37 cm² g^-1). From the confidence limit contour plot we can see that such a high value is ruled out. If we force a non-porous model to have this optical depth value, here is the best-fit model.

[14.87:15.13]
v_inf=2250
β=1
powerlaw continuum, n=2; norm=1.71e-3
q=0
h_inf=0
taustar=5.30
u_o=0.990 +/- (0.665:0.990)
norm=5.36e-4 +/- (5.16e-4:5.57e-4)
rejection probability = 97% (C=344.36; N=308)

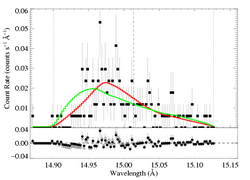
This fit is ruled out only at 97% confidence, formally. But the fit is clearly poor. And the low taustar fit - the global best-fit model - shown at the top of this page is preferred over this model with an even higher level of confidence (>99.99%), with ΔC > 64. Here are the two models plotted together:

Next, we fit isotropic porosity models to the data. And after that, anisotropic porosity models.

Back to main page.

last modified: 13 February 2009