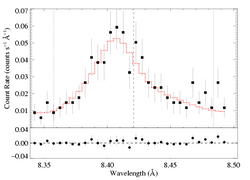
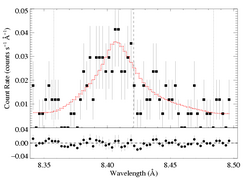
Mg XII 8.421 Angstroms

Non-porous models

Note: Both MEG and HEG are being fit simultaneously

Continuum fit on 8.25:8.35 and 8.50:8.60. For n=2, best-fit norm=1.65e-3. The 90% confidence limits on the normalization are +/-0.2e-3. And the best fit is formally a good fit.

Mg XII 8.421: non-porous MEG

Mg XII 8.421: non-porous HEG 		[8.34:8.50]
vinf=2250
β=1
powerlaw continuum, n=2; norm=1.65e-3
q=0
hinf=0
taustar=1.22   +/- (0.77:1.75)
uo=0.745   +/- (0.660:0.885)
norm=2.95e-5 +/- (2.71e-5:3.19e-5)
rejection probability = 16% (C=186.50; N=188)

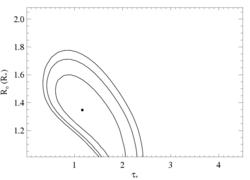
Here are the 68%, 90%, and 95% joint confidence limits on taustar and Ro based on fitting the MEG and HEG data together. The filled circle represents the best-fit model, shown as the red histograms on the above two plots.

Mg XII 8.421: joint uo taustar constraints using MEG+HEG data

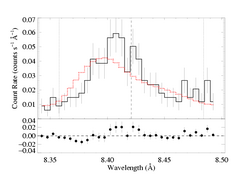
The above information (plots really, only; the fit didn't change) was updated on 5 Jan 09, but the information below, dates to May 2008.

The literature mass-loss rate implies a fiducial optical depth at the wavelength of this line of about taustar=4. From the confidence limit contour plot we can see that such a high value is ruled out. If we force a non-porous model to have this optical depth value, here is the best-fit model.

Mg XII 8.421: non-porous MEG with taustar=4
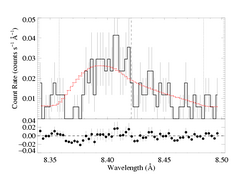
Mg XII 8.421: non-porous HEG with taustar=4 		[8.34:8.50]
vinf=2250
β=1
powerlaw continuum, n=2; norm=1.65e-3
q=0
hinf=0
taustar=4
uo=0.990   +/- (0.709:0.999)
norm=2.97e-5 +/- (2.79e-5:3.28e-5)
rejection probability = 63% (C=213.35; N=188)

So, ΔC~27, ruling this model out at >99.99%. Note that the best-fit value of uo is quite close to unity, but its value isn't tightly constrained at all. Finally, note that the Monte Carlo rejection probability is not all that high. Must be the poor S/N of the data...

Next, we fit isotropic porosity models to the data. And after that, anisotropic porosity models

 

Back to main page.

last modified: 5 January 2009