Exploring the effects of changing the opacity bridging law
in the Fe XVII 15.014 isoporous fit
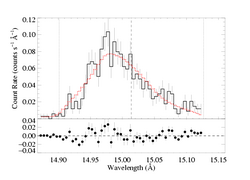
Because the best-fit models with porosity allowed tend to have hinf ~ 0, this comparison is best carried out for a high optical depth, high porosity model. We'll compare the taustar=8 fit, using both the MEG and HEG data.
Because the relevant integral can be done analytically in the case of the Rosseland opacity bridging law (1/(1 + tau_c)), for isoporous models, that has been our default. Here is the best-fit isoporous, Rosseland model with taustar=8 held fixed:
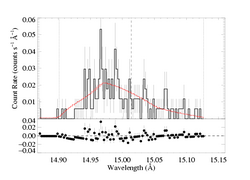
And here's the fit with the regular bridging law ((1 - exp(-tau_c))/tau_c):
So, the actual value (best-fit, and allowed range) of uo (and of course of the normalization too) does not change when we use the other bridging law. And the quality of the fit doesn't change much either. But the value of hinf (and the confidence range) does change substantially. To get the same effect on the profile shape, a larger porosity length is required when the regular (exponential) bridging law is used.
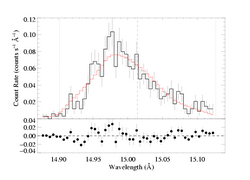
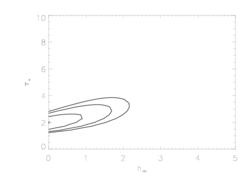
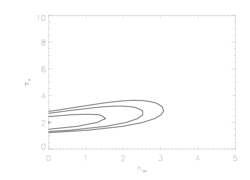
Another way of looking at the effect of the bridging law is to compare the confidence regions around the global best-fit model (which has a porosity length of zero) for the two cases.
So, here are the 68%, 90%, and 95% confidence limits for the Rosseland bridging law, which we've already shown here:
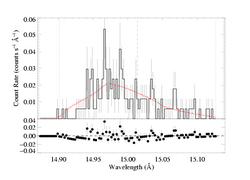
And here they are for the regular (exponential) bridging law:
Again, it makes sense that the same confidence limits extend to larger values of the porosity length in this case, since larger values of hinf are required to get the same profile morphology.
Finally, note the parameter settings (in the taustar=8 modeling):
- How we'd originally run the isoporous model (effectively, Rosseland, but only by default because we didn't specify "numerical").
- Explicitly choosing Rosseland (same result as above).
- Numerical calculation of regular bridging law (but physical parameters the same). The fit is worse, but not hugely (ΔC~6).
- Numerical calculation of regular bridging law (now with free parameters).
Back to main page.
last modified: 5 April 2008