Exploring the effects of varying beta
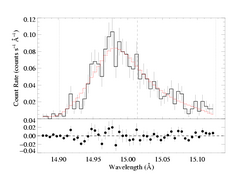
For the purposes of this exercise, we will fit the Fe XVII line at 15.014 over the wavelength range [14.87:15.13] and assume a terminal velocity of 2250 km/s - the baseline model. We will use only the MEG data and will not subtract any background (which makes this model fit very slightly different from the pure baseline case shown at the top of the main page (and many other places).
Here is the baseline model fit, shown on the background subtraction effects page.
We can use non-integer values of beta if we perform the optical depth integration numerically. So, parameter number 8 has to be set to 1, and then we can also set beta=0.8, for example. Below, we show this model, with a new normalization fit, but without any of the other parameters (taustar, uo) adjusted to improve the fit. Note that C has increased by about 7; this is pretty significant. The profile looks different. But it's hardly surprising. The value of beta affects the optical depth through the density (via mass continuity), and it also affects the Doppler shift of the emission at each location in the wind.

|
[14.87:15.13]
vinf=2250 β=0.8 powerlaw continuum, n=2; norm=1.91e-3 q=0 hinf=0 taustar=1.98 uo=0.657 norm=5.33e-4 rejection probability = 41% (C=103.34; N=102) |
Now we find the best-fit model with beta=0.8, allowing taustar and uo to be free parameters.
The differences in best-fit values and parameter ranges isn't all that small. Here's the reference fit (shown at the top of this page) with beta=1 again:
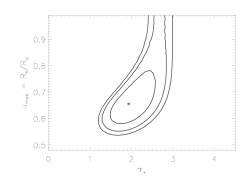
Here's how the confidence regions in taustar-uo space compare:
So, the value of beta does make a difference, both on the derived value and confidence range of taustar and of uo. Again, this isn't surprising. The Doppler shift of any volume element will depend on the velocity law. If we change this mapping by changing beta then there will be compensating changes in uo and if we change the run of density with radius by changing beta then there will be compensating changes in taustar. And not only will the best-fit models change with beta, but as the plots immediately above show, the shapes and position of the confidence regions in parameter space will also change.
For ζ Pup, there are a range of beta values in the literature, from beta=0.8 to beta=1.15 (even just looking at papers by the Munich group). The more recent determinations (e.g. Repolust et al.) have beta=0.9, but still... there's some uncertainty. Using beta=1 for our fitting seems reasonable, but we should keep the sensitivity to the value used in mind.
Back to main page.
last modified: 25 April 2008